Scientific and Engineering Workers: Education Supplies, Occupational Demands

A shorter version appears in Engineering Management Conference, 2002 (IEMC '02), vol. 2, pp: 544-549: http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1038493&tag=1

James Stodder, Lally School of Management and Technology

Rensselaer Polytechnic Institute at Hartford

275 Windsor Street, Hartford, CT 06120-2991, USA, stoddj@rpi.edu

Abstract: Recent studies by the National Science Foundation document the shortage of qualified scientific and engineering workers in the US. Because the demand for such workers is relatively insensitive to salaries, there is an emerging consensus that, rather than further subsidizing demand (and salaries), the US needs to subsidize supply. This paper argues that with regard to the Associate and level degrees for Engineers and Post-graduate degrees for Scientists, this consensus may be mistaken. A new data set compiled for this study relates educational supply to occupational demand through associated job "clusters" within 47 US states and Washington, DC. It finds that Post-graduate degrees in the Sciences are highly responsive to research spending, while Associate degrees in Engineering are highly responsive to salary -- much more responsive than demand. It follows that demand targeted to the appropriate incentive and degree level will be met with an elastic (responsive) supply. Such a policy would moderate salary inequalities, largely driven by demand for highly skilled workers. Across these states, the ratio between scientific-engineering graduate versus high-school graduate salaries is closely correlated with measures of overall wage inequality.

I. Introduction

Many economic commentators have expressed concern over shortages of qualified scientific and engineering (S&E) workers. This has been the subject of national studies by the National Science Foundation [14] and on state levels as well, for example in the Connecticut Employment and Training Commission [3]. The fact of these skill shortages is not difficult to document, but the best policy response is a question of real controversy.

A widely-discussed essay by Paul Romer [15], a leading figure in the economics of technological change, argues that the supply response of American higher education is not only inadequate, but "perverse" -- in the sense of withholding supply just as demand is rising. His thesis is that university politics have constrained Science and Engineering departments from adequately expanding their student enrollments, pushing them to instead over-invest in 'quality' and scholarly research.

The present paper will not address that controversial thesis. Two points of Romer's article that will be discussed, however, are his claims that:

· The educational supply of US-born scientific and engineering workers is highly inelastic (insensitive) to salary, substantially less elastic than industry demand.

· Because of this supply inelasticity, efforts to recruit more scientific and engineering talent by building up demand are destined to yield much higher salaries, but little in the way of higher supplies. Government and private industry should look more to directly stimulating supply. (See also Mincer [12].)

While not questioning Romer's conclusions on a nationwide labor-market basis, I find that these conclusions do not apply on the state or regional level within the US, and do not hold for particular sectors of scientific and engineering workers.

The present study finds that in the Sciences, Bachelor's and Post-Graduate degrees show more supply than demand response from R&D expenditures. In the broad Engineering and Electrical Engineering specialties, by contrast, the salary elasticity for Associate degree supply is much greater than that for industrial demand. Thus, the supply of S&E workers is more market sensitive than demand at these degree levels and for these incentives. Increased market demand, if it can be closely targeted to these degree levels and rewards, is likely to meet with an encouraging supply response.

High supply elasticities suggest that subsidies for salaries or R&D, if explicitly tied to early in-state career choices, could be highly productive. Such subsidies are a demand side "quick fix" -- calling forth greater supply, not through deep overhauls of academic structures, but by targeted market subsidies. There are other implications of this study that argue in the same direction -- for directing demand more on the more basic end of professional qualifications, to Associate degrees and short-term certificates:

· Many studies, for example the Battelle report [3], stress the need to expand business input into the education process, to craft educational outcomes more for industry uses. Such inputs are best concentrated on the earlier degree end of the higher educational process, where industry links are already strong and where outcomes are more rapidly achieved.

· Comparisons or benchmarking of leading research states, such as California, Maryland, Illinois, and Virginia, suggest their educational programs focus more resources toward the Associate degree and Certificate levels [3].

· Some richer states lag far behind in the provision of Associate degrees. Connecticut, for example, with the highest income per capita in the US, provided no Associate degrees in the Sciences in 1996-97. This argues again for expanding the resources for these programs, and refocusing business demand and involvement in these fields.

· This study finds that the gaps between unskilled (high-school diploma only) wages and the wages in these professional degree areas correlate strongly with the overall inequality of incomes. An expansion in Associate and certificate programs -- as opposed to more resources for the highest degrees -- would tend to moderate these wage gaps. The existence of a large wage gap also suggests that state resources are there to expand the more basic degrees.

The findings of this study show that something can be done about expanding educational supply in the short term, before tackling reform of the deeply embedded and complex structures of academia (tenure, research focus, etc.) Rather than contradicting Romer's thesis, the present study can be seen as a partial qualification, but also a confirmation of his basic argument. It is a qualification inasmuch as it shows that the market insensitivity of the US higher education does not hold everywhere for the supply of S&E workers. But it is a confirmation in that it finds

• for Post-graduate degrees in the basic sciences, supply is sensitive to research expenditures rather than to salary increases, thus confirming the research focus Romer cites.
• for Bachelors' degrees in engineering, the educational supply does appear "perverse," reacting to salary increases with fewer, not more degrees produced.
• that the supply of engineers is most sensitive to salary pressure where Romer would predict -- far from the ethos of the great research universities, in the Associate degree programs. Students in programs at the Associate and Certificate levels already have the shortest time-to-market, so we would expect to be more closely linked to regional demands.

These supply elasticities have clear policy implications. Wage and research-expenditure elasticities for the supplies of S&E workers at the appropriate levels -- Post-graduate for the Sciences, and Associate for Engineering -- are found to be several times higher than the demand elasticities. This implies that industry demands targeted to these degree levels, perhaps with provisions for continuing education, will meet with a robust supply response.

II. Four Educational/Occupational Clusters

Many different sorts of academic training are used for many sorts of jobs. How do we decide what these are, and thereby measure educational supply and occupational demand? Unlike the UK and many other West European countries [7], the US has no nationwide database of occupations sorted by comparable levels of skill -- the US sorting of Occupational Employment Statistics (OES) is merely by industrial area [5]. The lack of such a skills-based occupational listing is more than just an academic concern. Numerous empirical studies in the US and several different European countries show that educational mismatches -- employees who are inadequately trained or "overeducated" for their jobs -- are widespread and have significantly lowered the return to education in terms of wages and productivity [11].

To minimize this loss, and to help students plan their path from school to work, the state of Connecticut's Department of Labor has spent many years constructing its own grouping of Occupational Cluster [6] relating educational supplies and occupational demands. Lacking any comparable nationwide mapping, I will use these cluster definitions, and assume that these clusters are similar in every state. Supporting this assumption, I can show that the basic patterns of supply and demand within the US and Connecticut clusters are highly similar. That is, within each cluster, the state and the national vector of demand for different occupational specialties are correlated, as are their vectors of supply for different academic degrees. The correlation coefficients for these paired vectors are significant at the 5 percent level or better. For five of the six series examined, the correlation coefficient is significant at 0.1 percent. These state by state clusters -- drawn from sources [1], [5], [6], and [13] -- allow us to tie together, and then estimate, educational supplies and occupational demands.

The first grouping is the Sciences Cluster, containing the following occupational descriptions:

Table 1. Sciences Cluster

Biological Scientists

Chemists, Except Biochemists

Geologists, Geophysicists, and Oceanographers

Physicists and Astronomers

In Table 2., Engineering is a Macro-Cluster, or "cluster of clusters," with the following sub-clusters. One of its component clusters, Electrical Engineering, will be expanded below in Table 3.:

Table 2. Engineering Macro-Cluster

Sub-Cluster Titles

Electrical Engineering/Technology

Mechanical Engineering/Technology

Industrial Engineering/Technology

Civil Engineering/Technology

Architecture

Metallurgical Engineering/Technology

Chemical Engineering/Technology

Other Engineering Specialties

Table 3. Electrical Engineering/Technology Cluster

Computer Engineers

Electrical and Electronic Engineering Technicians and Technologists

Electrical and Electronic Engineers

Engineering, Mathematical, and Natural Sciences Managers

A full description of these clusters and their occupational and educational components is provided in

the Appendix, using national and state data. Constructing these clusters from the various data sets is a fairly tedious process. Nonetheless, if it shows the practicality of constructing a consistent national data set of educational supplies and occupational demands, it will constitute the main value of this paper.

III. Estimates of Supply and Demand

In the salary data from the OES [5] and ALMIS [1] data bases, there are only averages within each occupational specialty, rather than salaries at hiring. Such offer prices would be the obvious focus for an analysis of supply and demand. Instead, I use average salaries, weighted by the demand for new workers in particular occupations within each cluster. These "hiring-weighted averages" were in all cases slightly below these overall averages -- as one would hope for entry level positions.

A. Supply and Demand for Employees in the Sciences

Demand estimates for the Sciences are given in Table 4. The dependent variable is the proportion of new openings among scientific occupations in 1996-97. Demand and supply did show sensitivity to a variable that may be influenced by policy -- R&D spending as a portion of Gross State Product (GSP). In what follows, I will compare "elasticities" (sensitivities) of these R&D terms on the demand and supply sides.

Table 4: Scientists Demanded (All Degree Levels) Across US States, 1996-97

Dependent Variable: (DEMAND)	Job Openings in Sciences as Portion of Total Scientific Employment
EQUATION (#)	(1)	(2)
R-squared	0.2588	0.2457
Adjusted R-squared	0.1705	0.2122
F-statistic	2.9328	7.3293
Variables	Coefficient Estimates t-statistics
Constant	0.032251	0.024423
	1.677	5.781
State Personal Income	1.21E-08
	0.022
Average Salary Science	-2.48E-07
	-0.635
Science as Portion of Total State Employment	1.07164
	0.791
R&D/GSP	0.200316	0.193474
	1.491	1.823
Growth of GSP	0.313144	0.283168
	2.986	3.015

Note: (Applies to all subsequent tables.): T-stats. in italics. T-stat. is above a critical level when underlined as dashed, single, or double, for a 15%, 10%, or 5% level of statistical significance, respectively. There are 48 State Observations, plus DC. All data are from 1996-1997.

In Tables 5 and 6 below, I give the supply-side estimates for Bachelors' and Post-Graduate degrees in the Sciences, as a portion of the total workforce. (The results of the regressions on the supply of Associate Degrees were not highly significant, and are not reproduced here.) Although the R-squared is low, the R&D/GSP term is highly significant.

Note that any problem separately estimating the supply and demand equations -- the well known "identification problem" of econometric analysis -- does not arise in our case. The large gaps between state supplies and demands are in this sense fortuitous. The proportion of students supplied and employees demanded are not only quite different, they are even given different denominators in our estimates -- that of the total State Employment and total cluster employment, respectively.

Table 5. Scientists Supplied (Bachelor's) Across US States, 1996-97

Dependent Variable: (SUPPLY)	Bachelor's Degrees in Sciences, as Portion of Total State Employment
EQUATION (#)	(1)	(2)	(3)
R-squared	0.1218	0.0971	0.0736
Adjusted R-squared	0.0173	0.0355	0.0324
F-statistic	1.1653	1.5772	1.7873
Variables	Coefficient Estimates t-statistics
Constant	9.31E-04	6.31E-04	5.69E-04
	3.200	8.521	12.165
State Personal Income	-4.02E-09
	-0.479
Average Salary Science	-5.53E-09
	-0.935
Science Employment as Portion State Employment	-0.017812	-0.028922	-0.025419
	-0.869	-1.644	-1.468
R&D/GSP	4.30E-03	3.25E-03	2.82805E-03
	2.114	1.838	1.638
Growth of GSP	-1.30E-03	-1.57E-03
	-0.816	-1.070

Table 6: Scientists Supplied (Post-Graduate) Across US States, 1996-97

Dependent Variable: (SUPPLY)	Post Graduate Degrees in Natural Sciences as Portion of Total State Employment
EQUATION (#)	(1)	(2)	(3)
R-squared	0.178541	0.1710	0.172709
Adjusted R-squared	0.080749	0.1341	0.116303
F-statistic	1.82571	4.6405	3.06188
Variables	Coefficient Estimates t-statistics
Constant	5.30E-05	6.091E-05	4.75E-05
	0.939	6.853	1.055
State Personal Income	-3.22E-10
	-0.198
Average Salary Science	5.13E-10		3.26E-10
	0.446		0.303
Science Employment as Portion State Employment	1.98E-03	2.881E-03	2.41E-03
	0.498	0.876	0.660
R&D/GSP	7.75E-04	7.91E-04	7.40E-04
	1.963	2.411	1.988
Growth of GSP	-1.66E-04
	-0.539

Table 6 uses the regressions in Tables 4-5 to calculate demand and supply elasticities for R&D. The coefficient estimates taken from these tables are from those regressions with highest adjusted R-squareds. All coefficients are significant at the 10 percent level or better. (Elasticities in this paper will be estimated at the minimum, median, mean, and maximum state figures, unless otherwise noted.)

In Table 7 below, elasticity terms are all far less than 1.0, indicating that a 1 percent increase in the portion of GSP devoted to R&D would lead to much less than 1 percent increase in the demand or supply for science workers.

Table 7: Scientists: Supply & Demand Elasticity with respect to Proportion of GSP used as R&D

-- States with Minimum, Median, Mean, and Maximum Values for this Proportion

		Minimum (S. Dakota)	Median (Alabama)	Mean (Virginia)	Maximum (New Mexico)
Dependent Variable:	New Openings as % Total Science Employment in State	4.000%	6.047%	3.333%	6.885%
Independent Variable:	R&D/GSP	0.350%	1.590%	1.969%	6.690%
	(a) Coefficient on Independent Variable	0.1935	0.1935	0.1935	0.1935
	(b) Independent/Dependent Variable	0.0875	0.2629	0.5907	0.9717
	(a) x (b) = DEMAND ELASTICITY of R&D:	0.0169	0.0509	0.1143	0.1880
Dependent Variable:	Science Bachelor's Degrees as % Total State Employment	0.0740%	0.0541%	0.0744%	0.0482%
Independent Variable:	R&D/GSP	0.350%	1.59%	1.969%	6.690%
	(a) Coefficient on Independent Variable	3.25E-03	3.25E-03	3.25E-03	3.25E-03
	(b) Independent/Dependent Variable	4.730	29.385	26.478	138.851
	(a) x (b) = SUPPLY ELASTICITY of R&D:	0.0154	0.0955	0.0861	0.4513
Dependent Variable:	Science Post-Grad Degrees as % Total State Employment	0.0129%	0.0067%	0.0084%	0.0149%
Independent Variable:	R&D/GSP	0.350%	1.59%	1.969%	6.690%
	(a) Coefficient on Independent Variable	7.91E-04	7.91E-04	7.91E-04	7.91E-04
	(b) Independent/Dependent Variable	27.20	237.29	234.64	449.76
	(a) x (b) = SUPPLY ELASTICITY of R&D:	0.0215	0.1875	0.1854	0.3553

These estimated elasticities indicate that a 100 per cent increase of R&D expenditures in median expenditure Alabama -- from 1.59 to 3.18 per cent -- would be predicted to increase the demand for scientists by 5.09 percent -- from our data value of 130, to 137. This same 100 percent increase in R&D would be predicted to proportionally increase the supply of science bachelor's degrees almost twice as much, by 9.55 percent -- from 969 to 1,062. For post-graduate degrees in the sciences, the proportional increase would be twice as great again, by 18.75 per cent -- from 120 to 132 degrees yearly. Note that the R&D elasticity estimates for post-graduate scientists in Table 7 are greater than the elasticities for Bachelors' degrees. We will not see this pattern repeated: unlike the case with these graduate degrees in the Sciences, the lower the degree level in Engineering, the higher its supply response -- to salaries. The fact that it is research rather than salary dollars that generate the high supply elasticities in Table 7 above, suggests that the motivation for scientists tends to be different than that for engineers. It is reasonable to find scientists more motivated by the opportunity for original research, and with that motivation increasing with their degree level.

There is one pattern of Table 7 that we will see repeated in all of our estimates to come, however -- supply sensitivity always trumps demand. This dominance of supply elasticity runs counter to national surveys of the market for scientific and engineering workers [14], [15]. Despite the appearance of a contradiction, however, there is no logical inconsistency between these two sets of findings. Because states can recruit potential science students from other states, it is reasonable to expect that the supply of science students for an individual state might well be more R&D-elastic than the supply of the nation as a whole. Indeed, there could be zero supply elasticity for the nation as a whole, but high elasticities for individual states.

A. Supply and Demand for Engineering

Table 8. Engineers Demanded (All Degree Levels) Across US States, 1996-97

Dependent Variable: DEMAND	Job Openings in Engineering as Portion of Total Engineering Employment
EQUATION (#)	(1)	(2)	(3)	(4)
R-squared	0.5210	0.5101	0.4832	0.4768
Adjusted R-squared	0.4640	0.4645	0.4480	0.4411
F-statistic	9.1370	11.1923	13.7143	13.3662
Variables	Coefficient Estimates t-statistics
Constant	0.043815	0.044364	0.046427	0.020584
	2.633	2.669	2.760	2.217
State Personal Income	7.12E-07	6.73E-07		3.45E-07
	1.617	1.535		0.856
Average Salary Engineering	-7.25E-07	-6.93E-07	-4.20E-07
	-1.782	-1.709	-1.135
Engineering Employment as Portion of Total State Employment	0.883958	0.677213	0.729484	0.433221
	2.676	2.666	2.855	2.019
R&D/GSP	-0.113651
	-0.979
Growth of GSP	0.330154	0.332133	0.306848	0.346742
	4.540	4.571	4.271	4.704

In the remainder of this paper, we give Supply estimates only for the lower-level (and more elastic) degrees. In Table 8 above, demand estimates for Engineering show a significantly negative coefficient on average salary. The coefficient on Personal Income is positive and somewhat significant, implying that wealthier states demand more engineering services. The significant coefficient on salary will allow us to compare its supply and demand elasticities. R&D spending across states does not appear a significant determinant of demand for engineers, as it was in the demand for scientists. This finding also holds true for the supply estimates below.

In Table 9 below, the estimates for Bachelor's degrees in Engineering give Salary a significantly negative coefficient. This supports Romer's [15] claim that the academic supply of engineers is "perverse" -- granting fewer degrees as more are demanded. None of the other terms is significant.

Table 9. Engineers Supplied (Bachelor's Degrees) across US States, 1996-97

Dependent Variable: SUPPLY	Bachelor's Degrees in Engineering, as Portion of Total State Employment
EQUATION (#)	(1)	(2)	(3)
R-squared	0.1569	0.0971	0.0965
Adjusted R-squared	0.0565	0.0355	0.0564
F-statistic	1.5632	1.5773	2.4030
Variables	Coefficient Estimates t-statistics
Constant	0.02464	0.022401	0.022402
	4.181	4.034	4.078
State Personal Income	-7.82E-08	-2.53E-08
	-0.501	-0.165
Average Salary Eng.	-2.58E-07	-2.60E-07	-2.71E-07
	-1.789	-1.799	-2.166
Engineering Employment as Portion State Employment	0.064637	0.143679	0.142897
	0.552	1.698	1.710
R&D/GSP	0.060139
	1.463
Growth of GSP	-0.02254
	-0.875

In the next Table 10, the supply estimates for Associate's degrees in Engineering show personal income and hiring-weighted salary as the only significant terms. And unlike the previous table for Bachelors' degrees, salary here has the expected positive sign. But it is interesting that the supply of associate degrees is negatively related to the state's personal income. Supplying engineers is apparently not something most wealthier states are inclined to do, at least at the Associate level.

Table 10. Engineers Supplied (Associate Degrees) across US States, 1996-97

Dependent Variable: SUPPLY	Associate Degrees in Engineering as Portion of Total State Employment
EQUATION ( #)	(1)	(2)	(3)
R-squared	0.1670	0.1473	0.1415
Adjusted R-squared	0.0679	0.0892	0.1033
F-statistic	1.6842	2.5340	3.7078
Variables	Coefficient Estimates t-statistics
Constant	9.06E-03	5.43E-03	2.63E-03
	0.838	0.545	0.310
State Personal Income	-7.66E-07	-7.11E-07	-7.03E-07
	-2.676	-2.591	-2.585
Average Salary Eng.	3.68E-07	4.03E-07	4.83E-07
	1.390	1.559	2.275
Engineering Employment as Portion State Employment	0.179309	0.083327
	0.835	0.549
R&D/GSP	-0.020757
	-0.275
Growth of GSP	-0.045596
	-0.965

Using the coefficients on salary from Tables 8 and 10 with highest t-stats gives the values in Table 11. A 10 percent increase in Minnesota's hiring-weighted salary (from $50,849 to $55,934) results in a 5.75 percent fall in Total Engineering Demand, but a 22.7 percent rise in the supply of Associate Engineering degrees. This means a fall from 2,454 to 2,313 in openings for engineers (a loss of 141), but a rise in supply of Associate Degrees from 11,402 to 13,990 (a gain of 2,588).

Table 11: Engineers: Supply & Demand Elasticities with respect to Average Hiring Salary

-- States with Minimum, Median ≈ Mean, and Maximum Salary, 1996-97.

		Minimum (Montana)	Median ≈ Mean (Minnesota)	Maximum (New Jersey)
Dependent Variable:	New Openings as % Total Engineering Employment in State	4.099%	6.416%	3.995%
Independent Variable:	Hiring-Weighted Average Engineering Salary	$ 40,499	$ 50,849	$ 59,849
	(a) Coefficient on Independent Variable	-7.25E-07	-7.25E-07	-7.25E-07
	(b) Independent/Dependent Variable	988,074	792,569	1,498,204
	(a) x (b) = DEMAND ELASTICITY:	-0.716	-0.575	-1.086
Dependent Variable:	Engineering Associate Degrees as % Total State Employment	0.509%	1.083%	0.964%
Independent Variable:	Hiring-Weighted Average Engineering Salary	$ 40,499	$ 50,849	$ 59,849
	(a) Coefficient on Independent Variable	4.83E-07	4.83E-07	4.83E-07
	(b) Independent/Dependent Variable	7,951,176	4,695,632	6,206,406
	(a) x (b) = SUPPLY ELASTICITY:	3.840	2.268	2.998

B. Supply and Demand for Electrical Engineering Workers

In the following estimate of Table 12, Electrical Engineering Demand is sensitive to salary. State Personal Income is weighted positively for demand. All other coefficients have the expected sign, except for R&D. This was not significant, and so was dropped as likely collinear with Employment.

Table 12: Electrical Engineers Demanded (All Degrees) across US States, 1996-97

Dependent Variable: DEMAND	Job Openings in Electrical Engineering as Portion of Total EE Employment
EQUATION (#)	(1)	(2)	(3)
R-squared	0.4944	0.4436	0.325
Adjusted R-squared	0.4343	0.4056	0.295
F-statistic	8.2154	11.6918	10.819
Variables	Coefficient Estimates t-statistics
Constant	0.047581	0.052971	0.071972
	2.565	2.911	3.861
State Personal Income	7.83E-07
	1.426
Average Salary EE	-8.34E-07	-5.64E-07	-8.11E-07
	-2.027	-1.451	-1.956
EE Employment as Proportion of Total State Employment	1.73988	1.32317	1.77094
	3.161	3.454	4.590
R&D/GSP	-0.230401
	-1.523
Growth of GSP	0.303377	0.283524
	3.163	3.066

In the following regression on the supply of Associate Degrees, in Table 13, we again see supply negatively correlated with state income, and positively related to hiring weighted salary. As before, the Associate level shows more salary sensitivity than higher level degrees (regressions not shown).

Table 13. Electrical Engineers Supplied (Associate Degrees) across US States, 1996-97

Dependent Variable: SUPPLY	Associate Degrees in Electrical Engineering as Portion Total State Employment
EQUATION (#)	(1)	(2)	(3)
R-squared	0.20868	0.19398	0.173
Adjusted R-squared	0.11447	0.13902	0.116
F-statistic	2.21512	3.52968	3.064
Variables	Coefficient Estimates t-statistics
Constant	2.89E-04	2.07E-04	1.35E-04
	1.236	0.979	0.666
State Personal Income	-2.15E-08		-1.91E-08
	-3.113		-2.909
Average Salary EE	7.12E-09	7.52E-09	9.38E-09
	1.372	1.479	1.935
EE Employment as Portion of Total State Employment	9.26E-03	6.17E-03
	1.335	1.405
R&D/GSP	-4.87E-04	-1.98E-08	1.18E-03
	-0.255	-3.051	0.892
Growth of GSP	-1.06E-03
	-0.873

In Table 14, supply is about twice as elastic as demand. A 10 percent increase in salary for mean-salary Maine (from $49,263 to $54,189) would cause an 8.07 percent fall in job openings (from 799 to 716) annually, but a 16.66 percent rise in Associate degrees supplied (from 121 to 141). These findings on elasticity have clear policy implications: pushing inelastic demand along the more elastic supply curve would make it possible get more added output per extra dollar spent.

Table 14. Electrical Engineering, Elasticities with respect to Average Hiring Salary

-- States with Minimum, Median, Mean, and Maximum Salary, 1996-97.

		Minimum (Montana)	Mean (Maine)	Median (New Mexico)	Maximum (Idaho)
Dependent Variable:	New Openings as % Electrical Engineering Employment in State	4.138%	5.091%	6.026%	7.682%
Independent Variable:	Hiring-Weighted Average Electrical Engineering Salary	$38,669	$49,263	$49,599	$58,970
	(a) Coefficient on Independent Variable	-8.34E-07	-8.34E-07	-8.34E-07	-8.34E-07
	(b) Independent/Dependent Variable	934,504	967,667	823,059	767,629
	(a) x (b) = DEMAND ELASTICITY:	-0.779	-0.807	-0.686	-0.640
Dependent Variable:	Elect-Engineer Associate Degrees as % Total State Employment	1.86E-05	2.22E-04	2.68E-04	3.60E-04
Independent Variable:	Hiring-Weighted Average Electrical Engineering Salary	$38,669	$ 49,263	$49,599	$58,970
	(a) Coefficient on Independent Variable	7.52E-09	7.52E-09	7.52E-09	7.52E-09
	(b) Independent/Dependent Variable	2,082,090,992	221,541,164	184,801,732	163,835,348
	(a) x (b) = SUPPLY ELASTICITY:	15.657	1.666	1.390	1.232

III. Within-State Income Inequalities

There is no question that the demand for Engineering and Science workers is increasing in the advanced industrial countries [14]. This growing disparity of supply and demand has implications for disparities in income. Thus most economists explain the large increase in US income inequality since the early '70s as driven largely by increased demand for technologically skilled workers [10].

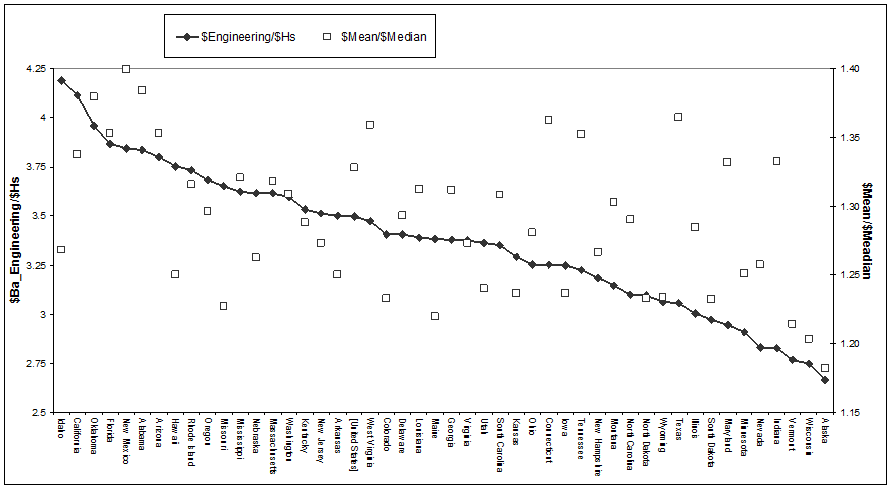
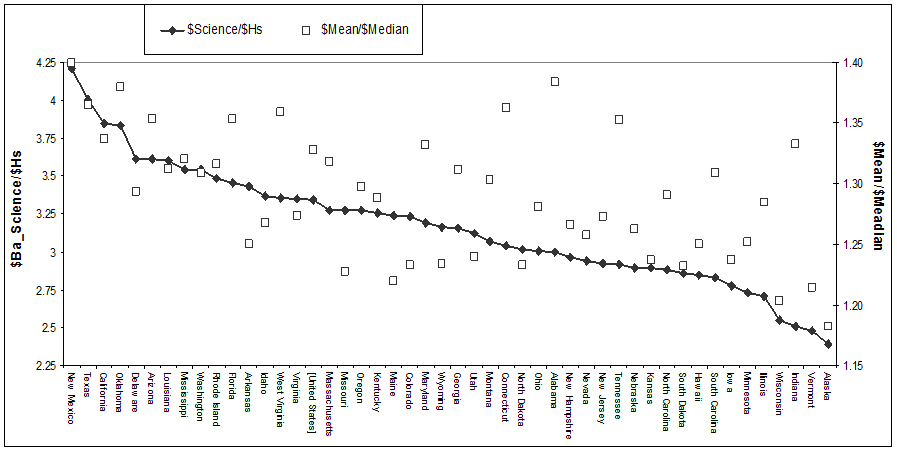
Fig. 1 tracks the correlation between two inequality ratios on a state by state basis. The first is the ratio of mean household income to its median -- that household at the 50th percentile of the distribution. The second is the ratio between the salary of science professionals, and the salary of the average high-school graduate with no further education [4]. The Pearson correlation coefficient between these two series is 0.59, with a significance level of 0.1 percent. (Similar correlations between inequality rations can be shown for engineering as a whole, and for electrical engineering, where the significance level is always at most 5 percent.)

Correlations do not show the direction of causality, of course. There is, however, evidence that the distribution of skill influences the distribution of salaries. Comparing Germany and the US, for example, a recent study finds that Germany's distribution of wages can be partly explained by its more equal distribution of skills. The paper's estimates imply that if the Germany had a dispersion of skills as wide as that actually found in the US, German inequality (as measured by the standard deviation of its log-wages) would increase by 3.9 percent. Similarly, if the US had a German dispersion of skills, its wage inequality would fall by 4.7 percent [8].

IV. Conclusions, Implications

The evidence shows that for some scientific and engineering labor markets, educational supply may be more salary-elastic than industry demand. In such cases, subsidizing demand rather than supply will provide more employees at reasonable cost in the shortest possible time.

Directly subsidizing supply yields a longer term increase the stock of human capital and reduction in skill differentials, with lags of up to a decade [12]. If short-term supply elasticity is low, there is evidence that investment in public education has a high long-term social return, and lessens income inequalities and skill premia [2], [9], [16].

The principal accomplishment of this paper may not be its economics, which is elementary, but rather its accounting -- which is tedious but necessary. That the US, unlike several European countries, has no cluster-integrated nation-wide database of occupations [7] is a problem and an opportunity. The "cluster" analysis presented here makes the case that there are substantial gains to constructing and analyzing such a data set. This paper has only scratched the potential of this large database -- only for three educational/occupational clusters, and only for one year. There are dozens of clusters yet to be defined, complied, and analyzed.

Fig. 1: Salary Ratios -- Science Bachelor's over High School Graduates, Mean over Median, by State 1996-97

Sources (all figures): OES database; Census tapes (DDB: PPINC*DDB(0), MDB: PPINC*DDB)

Figure 2: Salary Ratios: Engineer's Bachelor's Over High School Graduates, Mean Over Median, by State

Pearson Correlation Coefficient: 0.461 (p = 0.001)

Spearman's Rank Correlation: 0.419 (p = 0.003)

Figure 3: Salary Ratios: Elect. Engineer's Over High School Graduates, Mean Over Median, by State

Pearson Correlation Coefficient: 0.311 (p = 0.031)

Spearman's Rank Correlation: 0.315 (p = 0.029)

Sources: Same as previous Figure.

Acknowledgment: Support for this study was provided by the Connecticut Economic Resource Center, http://www.cerc.com. The views expressed are the responsibility of the author alone.

Appendix: Five Data Sets Integrated, Four Clusters Examined

Note: The new integrated national data set assembled for this report is very extensive, with several thousand records in each of the five national data sets that were used to compile it. Data are only presented in their final extracted form here -- the form used for this report's calculations. The complete data set has been assembled into spreadsheet form, on CD-ROM, and is available from the author.

A.1 The Five Data Sets

Just as poor materials can undermine the best design, it is useless to do detailed empirical analysis with inadequate data. To understand the relation of educational supply and occupational demands, I am comparing

1) Educational Program Completions and School Spending;

2) Salaries of High-school Graduates;

3) Occupational Demands;

4) Wages in those Occupations; and

5) Occupational Clusters, relating 1) and 3)

To construct the data set used for this paper, I have integrated 5 different data sets, no two of which were designed to be strictly comparable.

Looking at 1) data on educational supply, state-by-state comparability is excellent. The National Center for Educational Statistics (NCES) [13] offers the Integrated Post-secondary Education Data System (IPEDS) at nces.ed.gov/ipeds/. This is a truly national source on completions, by program and level of degree awarded, going from the present back to the late 1980s.

For 2) salaries of high-school graduates on a state-by-state level, census tapes [4] averaged for 1992-94 and 1995-97 were used, extracted via the "ferret" program at www.census.gov.

When one comes to the labor market data, large gaps begin to appear. For estimates of 3) annual occupational demands, the source is ALMIS (American Labor Market Information System), almis.dws.state.ut.us/, [1]. This gives state employment levels for thousands of job descriptions. However, several large industrial states (New York, Pennsylvania, and Michigan) do not provide ALMIS with their data, nor does Washington D.C. These four data "holes" exist in everything that follows.

For 4) average occupational salaries, one must go to the Occupational Employment Statistics (OES) [5] page of the Bureau of Labor Statistics, stats.bls.gov/oeshome.htm. These average salaries do not represent the salary at which new labor was hired, and are thus not strictly the wage component of labor demand. In order to approximate this wage however; the occupational weightings used in the cluster were those of the annual demands listed by ALMIS [1], shown in 3) above.[1] Using the actual demand weights for each cluster -- rather than un-weighted average salaries -- proved very important in getting reasonable results for the regression estimates.

Finally, I come to the issue posed in 5) the appropriate clusters of Supply and Demand. Which educational programs and job descriptions should we fit together? To answer this, I have used the Occupational Cluster definitions developed by the Connecticut State Department of Labor. These Clusters are laid out a 1996 publication [6]. The most recent data available for all four data sets is based on the 1996-97 academic and fiscal year.

A.2 Four Clusters in Science and Engineering

A.2.1 Definition of the Science Cluster

I have broken out two "hard" sciences, the Physical Sciences and Life Sciences Cluster. This reflects an emphasis on fundamental research, rather than on technical implementation. The overlap of the OES, ALMIS and Connecticut DoL data sets allows a relatively limited focus, on just four occupational categories. As defined by the Connecticut State Department of Labor, the Science Cluster is made up of the following component occupational clusters. Note that the two series are highly correlated, at the 2 percent level of significance.

Table A.1. Occupational Classifications of Sciences Cluster: OES [5], ALMIS [1], CT DoL [6], 1996-97

Cluster Code	OES Code	OES Title, OES	Almis, Connecticut DoL Title	US Demand	Connecticut Demand
1205	24308	Biological Scientists	Biological scientists	2,640	190
1206	24105	Chemists, Except Biochemists	Chemists	3,650	140
1206	24111	Geologists, Geophysicists, and Oceanographers	Geologists, geophysicists, and oceanographers	1,710	20
1206	24102	Physicists and Astronomers	Physicists and astronomers	380	10
			ALMIS TOTAL DEMAND	8,380	360
			Connecticut Dol Total Demand		500
			Data Set Connecticut Coverage, ALMIS/ Connecticut DoL		72.0%
Pearson Correlation Coefficient, US and CT demands: 0.944 (p-value = 0.016)

The next order of business is to gather the occupations listed in the Connecticut Department of Labor (Connecticut DoL) definition of this macro-cluster [6] with those occupations listed in the national ALMIS database [1]. Overlap is not perfect. In order to get data on wages; I have to then compare this national set with the occupations listed in the OES database [5]. The complete listing of the intersection of these three data sets in the Technology cluster, and their US and Connecticut job openings for 1996-97, is given in Table A.1. Note that changes in the Cluster Code, the first column, are reflected in changes in the font color.

Notice also that whenever there is a discrepancy in the job titles -- apart from the mere capitalization of letters or ordering of titles -- the classification titles are underlined. The left column shows the titles of the Bureau of Labor Statistics OES and its Occupational Classification Code (OCC) [5]. The right column shows those used by both ALMIS [1] and the Connecticut Department of Labor [6]. For the most part these offer little opportunity for confusion.

The final rows compare the Total Demand, or number of job openings in 1996-97, as accounted both by this merged data set, and by the Connecticut DoL set [6]. We see that about 64% of the job openings accounted for by Connecticut have been preserved in the transition to a national system. A similar percentage of Data Set Coverage will be seen in the other clusters to follow. Some loss is unavoidable, until a nationally integrated data system for occupational demands is instituted.

Next we come to the CIP (Classification of Instructional Programs) Codes given by the national IPEDS (Integrated Post-secondary Data Set) [13]. Here, the codes used nationally and by Connecticut are identical. Again, note at the bottom of Table A.2, that the structure of relative completions in the US and CT supply is highly similar, with a correlation coefficient significant at the 0.01 percent level.

Table A.2. Program Completions in Sciences cluster: IPEDS [13] and Connecticut DoL [6], 1996-97

Cluster Code	CIP code	CIPTITLE	US Supply	CT Supply
1205	26.0101	Biology, General	53443	566
1205	26.0401	Cell Biology	478	13
1205	26.0402	Molecular Biology	1081	120
1205	26.0499	Cell and Molecular Biology, Other	1633	42
1205	26.0501	Microbiology/Bacteriology	3359	8
1205	26.0608	Neuroscience	578	21
1205	26.0616	Biotechnology Research	259	7
1205	26.0702	Entomology	389
1205	26.0704	Pathology, Human and Animal	166	12
1205	26.0705	Pharmacology, Human and Animal	426	7
1205	26.9999	Biological Sciences/Life Sciences, Other	2234	6
1205	30.0101	Biological and Physical Sciences	9186
1205	51.1307	Medical Immunology	44	10
1205	51.1308	Medical Microbiology	208	0
1206	40.0101	Physical Sciences, General	1491	22
1206	40.0601	Geology	4182	21
1206	40.0603	Geophysics and Seismology	177
1206	40.0699	Geological and Related Sciences, Other	302	17
1206	40.0703	Earth and Planetary Sciences	829	19
1206	40.9999	Physical Sciences, Other	594	68
		IPEDS Total Completions	81059	959
		Connecticut DoL Total** Completions 1503
		Data set Coverage, IPEDS Connecticut /Connecticut DoL 63.81%
Pearson Correlation Coefficient, US and CT supplies: 0.991 (p-value = 0.000)

A.2.2 Definition of Engineering Cluster

This is a broad macro-cluster, of eight component clusters:

Table A.3. ENGINEERING MACRO-CLUSTER, Connecticut Department of Labor [6]

Sub-Cluster Titles	Cluster Titles
Electrical Engineering/Technology	1101
Mechanical Engineering/Technology	1102
Industrial Engineering/Technology	1103
Civil Engineering/Technology	1104
Architecture	1105
Metallurgical Engineering/Technology	1106
Chemical Engineering/Technology	1107
Other Engineering Specialties	1108

Dozens of job descriptions are spread over these clusters. Of these, the following jobs are covered jointly by our first three data sets. Note at the bottom of Table A.3, that the structure of relative occupational demand in the US and CT supply is highly similar, with a correlation coefficient significant at the 0.01 percent level.

Table A.4. Occupational Classifications of Engineering Cluster:

OES [5], ALMIS [1], CT DoL [6], 1996-97

Cluster code	OES code	OES Title	Almis Title	US Demand	CT Demand
1101	22.127	Computer Engineers	Computer engineers	25,000	340
1101	22.505	Electrical and Electronic Engineering Technicians and Technologists	Electrical and electronics engineers	19,720	210
1101	22.126	Electrical and Electronic Engineers	Electrical and electronic technicians and technologists	12,130	180
1101*	13.017*	Engineering, Mathematical, and Natural Sciences Managers	Engineering, science, and computer systems managers	6,840	69
1102	22.102	Aeronautical and Astronautical Engineers	Aeronautical and astronautical engineers	1,010	40
1102	22.138	Marine Engineers	Marine Engineers	320	10
1102	22.135	Mechanical Engineers	Mechanical engineers	8,130	180
1102	22.117	Nuclear Engineers	Nuclear engineers	430	10
1103*	13.017*	Engineering, Mathematical, and Natural Sciences Managers	Engineering, science, and computer systems managers	6,840	69
1103	22.128	Industrial Engineers, Except Safety	Industrial engineers, except safety engineers	3,890	70
1104	22.121	Civil Engineers, Including Traffic	Civil engineers, including traffic engineers	8,170	100
1104*	13.017*	Engineering, Mathematical, and Natural Sciences Managers	Engineering, science, and computer systems managers	4,560	46
1104	22.521	Surveying and Mapping Technicians	Surveyors	2,010	20
1105	22.302	Architects, Except Landscape and Marine	Architects, except landscape and marine	3,920	40
1105	22.308	Landscape Architects	Landscape architects	710	10
1106	22.105	Metallurgists and Metallurgical, Ceramic, and Materials Engineers	Metallurgists and metallurgical, ceramic, and materials engineers	610	20
1107	22.114	Chemical Engineers	Chemical engineers	2,190	20
			ALMIS Total Demand	106,910	1,434
			Connecticut DoL Total 1,960
			Data Set Connecticut Coverage, ALMIS/Connecticut DoL 73.2%
Pearson Correlation Coefficient, US and CT supplies: 0.997 (p-value = 0.000)

(*) Note: Engineering, Mathematical, and Natural Sciences Managers (OES Code 13017) are accounted as allocated between Clusters 1101, 1103 and 1104, Electrical Engineering, Industrial Engineering, and Civil Engineering, respectively. They are allocated in proportions of 0.3, 0.3 and 0.2, again, respectively. (The remaining 0.2 is allocated to Cluster 1503, Mathematical Specialties.) This is the allocation used by the Connecticut Department of Labor.

The educational specialties within this cluster are extremely diverse. Over seventy listings are given in the Connecticut DoL tables, although, as with the labor demand data above, the final rows of Table 6 show that 73% of the DoL listings are captured by the IPEDS [13] data. Again, the correlation between the two series is significant at 0.01 percent.

Table A.5. Program Completions in Engineering cluster: IPEDS [13], Connecticut DoL [6], 1996-97

Cluster code	CIP code	CIPTITLE	US Supply	CT Supply
1101	14.0901	Computer Engineering	3939	59
1101	14.1001	Electrical, Electronics & Communication	21976	194
1101	15.0301	Computer Engineering Tech./Technician	4033	81
1101	15.0303	Elec., Electronic & Comm. Engin. Tech.	17230	131
1101	15.0304	Laser and Optical Tech./Technician	208	1
1101	15.0399	Electrical & Electronic Engin.-Related Tech	9383	57
1101	15.0402	Computer Main. Tech./Technician	3907	188
1102	14.0201	Aerospace, Aeronautical and Astronautic	2177
1102	14.0301	Agricultural Engineering	901
1102	14.1101	Engineering Mechanics	344
1102	14.1901	Mechanical Engineering	18341	208
1102	14.2201	Naval Architecture & Marine Engineering	330	7
1102	14.2301	Nuclear Engineering	462
1102	14.2401	Ocean Engineering	273	1
1102	15.0403	Electromechanical Tech./Technician	1629
1102	15.0404	Instrumentation Tech./Technician	817
1102	15.0405	Robotics Tech./Technician	731
1102	15.0801	Aeronautical & Aerospace Engineering Tec	751	1
1102	15.0803	Automotive Engineering Tech./Technician	1124	30
1102	15.0805	Mechanical Engineering/Mechanical Tech.	3033	63
1102	15.0899	Mechanical Engineering-Related Tech, Oth	1040	2
1102	41.0204	Industrial Radiologic Tech./Technician	22
1102	41.0205	Nuclear/Nuclear Power Tech./Technician	102	9
1103	14.1701	Industrial/Manufacturing Engineering	6147	78
1103	14.3001	Engineering/Industrial Management	1204
1103	15.0603	Industrial/Manufacturing Tech/Technician	4392	35
1103	15.0699	Industrial Product. Technol./Techn, Oth.	1241	120
1104	14.0801	Civil Engineering, General	14982	94
1104	15.0201	Civil Engineering/Civil Tech./Technician	1976	8
1104	15.1001	Construction/Building Tech./Technician	2116	7
1104	15.1102	Surveying	574
1105	4.0201	Architecture	6726	72
1105	4.0401	Architectural Environmental Design	771	2
1105	4.0501	Interior Architecture	1047	21
1105	4.0601	Landscape Architecture	1259	12
1105	4.9999	Architecture and Related Programs, Other	771	7
1105	15.0101	Architectural Engineering Techno/Tech	2014	26
1106	14.1801	Material Engineering	1329	2
1106	14.2001	Metallurgical Engineering	424	13
1106	15.0611	Metallurgical Tech./Technician	87
1107	14.0701	Chemical Engineering	8511	42
1107	41.0301	Chemical Tech./Technician	579	6
1108	14.0101	Engineering, General	5005	22
1108	14.0501	Bioengineering & Biomedical Engineering	1645	9
1108	14.1201	Engineering Physics	393	19
1108	14.1301	Engineering Science	670	27
1108	14.1401	Environmental/Environmental Health Engin	2050	25
1108	14.2701	Systems Engineering	1008	1
1108	14.2901	Engineering Design	15
1108	14.3101	Materials Science	329	5
1108	14.3201	Polymer/Plastics Engineering	133
1108	14.9999	Engineering, Other	2341	32
		IPEDS Total Completions: 162,492 Connecticut DoL Total** Completions: Data Set Coverage, Connecticut Total/ Connecticut DoL:		1,717 1,365 126%
Pearson Correlation Coefficient, US and CT demands: 0.991 (p-value = 0.000)

A.2.3 Definition of Electrical Engineering Cluster

Electrical Engineering has generated particular interest as the area of engineering most closely associated with computer and related technologies. The overlap of our three labor market data sets shows the following demand count, with the correlation between the national and state series significant at 0.1 percent.

Table A.6. Occupational Classifications - Electrical Engineering Cluster:

OES [5], ALMIS [1], CT DoL [6], 1996-97

Cluster Code	OES Code	OES Title	Almis Title	US Demand	CT Demand
1101	22.127	Computer Engineers	Computer engineers	25,000	340
1101	22.505	Electrical and Electronic Engineering Technicians and Technologists	Electrical and electronic technicians and technologists	12,130	180
1101	22.126	Electrical and Electronic Engineers	Electrical and electronics engineers	19,720	210
1101	13.017	Engineering, Mathematical, and Natural Sciences Managers	Engineering, science, and computer systems managers	22,800	230
			ALMIS Total Demand	79,650	960
			Connecticut DoL Total Demand		880
			Data Set Connecticut Coverage ALMIS/Connecticut DoL		109.1%
Pearson Correlation Coefficient, US and CT demands: 0.994 (p-value = 0.001)

The data on program completions are as follow, with the correlation between the US and CT series significant at 0.01 percent.

Table A.7. Program Completions in Electrical Engineering cluster:

IPEDS [13]Connecticut DoL [6], 1996-97

Cluster code	CIP Code	CIP TITLE	US Supply	CT Supply
1101	14.0901	Computer Engineering	3,939	59
1101	14.1001	Electrical, Electronics and Communication Engineering	21,976	194
1101	15.0301	Computer Engineering Tech./Technician	4,033	81
1101	15.0303	Electrcial, Electronic and Communications Engin. Tech./Technician	17,230	131
1101	15.0304	Laser and Optical Tech./Technician	208	1
1101	15.0399	Electrical and Electronic Engineering-Related Technol./Technician	9,383	57
1101	15.0402	Computer Main. Tech./Technician	3,907	188
		IPEDS Total Completions	60,676	711
		Connecticut DoL Total** Completions		384
		Data Set Connecticut Coverage, IPEDS/Connecticut DoL		185.16%
Pearson Correlation Coefficient, US and CT supplies: 0.955 (p-value = 0.000)

In this assembly of multi-state supply and demand data, I have based our definition of clusters on the extensive research and practical experience of the Connecticut Department of Labor [6]. How comprehensive is this new multi-state data set? To compare it to the individual data sets of all 50 states is neither practical nor important at this point. What I have done is to compare its coverage with the published records of the DoL.

To summarize, the multi-state data set I have assembled covers about 2/3 of the occupational listing and labor demand categories of the Connecticut DoL data [6]. When it comes to the school completions data, however, the new data set's coverage often has better coverage (over 100%) compared to data used by the Connecticut DoL in assembling its clusters. This greater coverage of the IPEDS [13] may result from its data having been updated more recently.

REFERENCES

[1] ALMIS (American Labor Market Information System), http://almis.dws.state.ut.us/.

[2] R.J. Barro, "Human capital and growth in cross-country regressions," Swedish Econ. Pol. Rev., Vol. 6, pp. 237-277, Autumn 1999.

[3] Battelle Consultants, "An information technology workforce strategy for the state of Connecticut," Connecticut Employment & Training Comm., Dec. 2000.

[4] Bureau of the Census, tapes on state high school grad. rates, via "ferret" extraction tool, http://www.census.gov.

[5] Bureau of Labor Statistics, Occupational Employment Statistics (OES), http://stats.bls.gov/oeshome.htm.

[6] Connecticut State Dept. Labor, "Making the future yours: a comparison of job openings and education and training graduates," 1996.

[7] P. Elias and A. McKnight, "Skill measurement in official statistics: recent developments in the UK and the rest of Europe," Oxford Econ. Paps., Vol. 3, pp. 508-540, 2001.

[8] R. Freeman and R. Shettkat, "Skill compression, wage differenttials, and employment: Germany vs. the US," Oxford Econ. Paps., Vol. 3, pp. 582-603, 2001.

[9] C. Goldin and L. Katz "America's graduation from high school: the evolution and spread of secondary schooling in the twentieth century", J. Econ. History, Vol. 58, pp. 345-374, June 1998.

[10] J. Greenwood, "The third industrial revolution: technology, productivity, and income equality," Fed. Resrv. Bank Cleveland, Econ. Review, Vol. 35, 1999.

[11] J. Hartog "Over-education and earnings: where are we, where should we go?" Econ. Educ. Rev., Vol. 19, pp. 131-147, April 2000.

[12] Jacob Mincer, "Investments in U.S. education and training as supply responses," Rsch. Labor Econ., Vol. 17; pp. 277-304, 1998.

[13] Natl. Center for Educational Statistics, "Integrated post-secondary education data system," http://nces.ed.gov/ipeds/.

[14] Natl. Science Fnd., "Science and Engineering indicators - 2000," Arlington, www.nsf.gov/sbe/srs/seind00/start.htm.

[15] P. Romer, "Should the government subsidize the supply or demand in the market for scientists and engineers?," Natl. Bur. Econ. Rsch., Working Paper No. 7723, 1999.

[16] K. Sylwester, "Can education expenditures reduce income inequality?" Econ. Educ. Rev., Vol.21, pp.43-

52, Feb. 2002.

A shorter version of this paper was printed in an IEEE conference volume.

Search for author “Stodder” at the conference site:

http://ieeexplore.ieee.org/xpl/tocresult.jsp?isnumber=22258

“Scientific-technical workers: education supplies, occupational demands”

Engineering Management Conference, 2002. IEMC '02. 2002 IEEE International

Volume: 2

Digital Object Identifier: 10.1109/IEMC.2002.1038493

Publication Year: 2002 , Page(s): 544-549 vol.2

---

[1] The occupations listed have slightly different names in OES [5] and in ALMIS [1]. Comparability is not aided, furthermore, by the fact that OES uses the numerical Occupational Classification Code (OCC), while ALMIS does not. In all cases surveyed, however, a clear title match was possible. Comparisons of particular ALMIS and OES occupational titles can be seen in the cluster definitions that follow.

** In the Connecticut Department of Labor (CT DoL) Tables [6], the Total count on program completions is given without graduate degrees. (The number of graduate degrees is listed separately.) The Connecticut DoL does this because many of those completing graduate programs are part time students, and already employed in their field. For purposes of widest comparison here, the number of all degrees was used to compute the Connecticut DoL Total**, as given above. In this paper's statistical work, I will break down total completions both ways, with and without graduate degrees.